バターワースフィルタ(Butterworth filter)は、
通過域で最大平坦な振幅特性を示すローパスフィルタです。
位相特性も線形に近いという特徴があります。
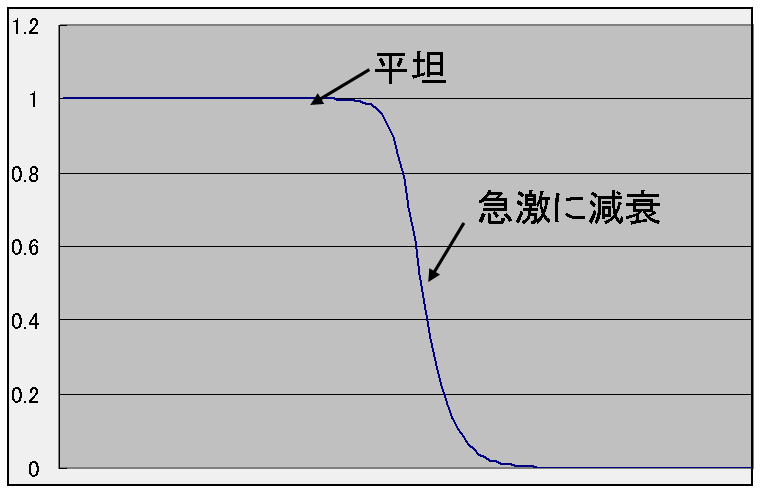 バターワースフィルタの周波数特性
バターワースフィルタの周波数特性
バターワースフィルタは以下のような周波数特性を持ちます。
この特性はω>1で急激に減衰していきます。
ωの変わりにω/ωcを代入することでカットオフ周波数ωcを任意に設定できます。
また、この伝達関数は1階から2n-1階までの全ての導関数がω = 0において0であるという性質を持っています。
この性質を最大平坦と呼びます。
図2に、例として、3次、5次、9次のバターワースフィルタの振幅特性を示します。
 3~9次のバターワースフィルタの周波数特性
3~9次のバターワースフィルタの周波数特性
|H(ω)|2の分母は2n次の多項式なので、
|H(ω)|2は2n個の極を持ちます。
この2n個の極は、
ω2n = -1より、以下のようになります。
この2n個の中から安定なn個の極を選び、
バターワースフィルタの極 s にします。
ただし、kは0~(n-1) / 2までの整数です。
決定された極配置から、バターワースフィルタの伝達関数H(s)は以下のようになります。
ただし、αk は以下の式で表される値です。
透過域/阻止域の周波数/リプル
(Ap, rs, ωp, ωs)
を仕様として与えたとき、
仕様を満たす最小の次数 N を求める方法について説明します。
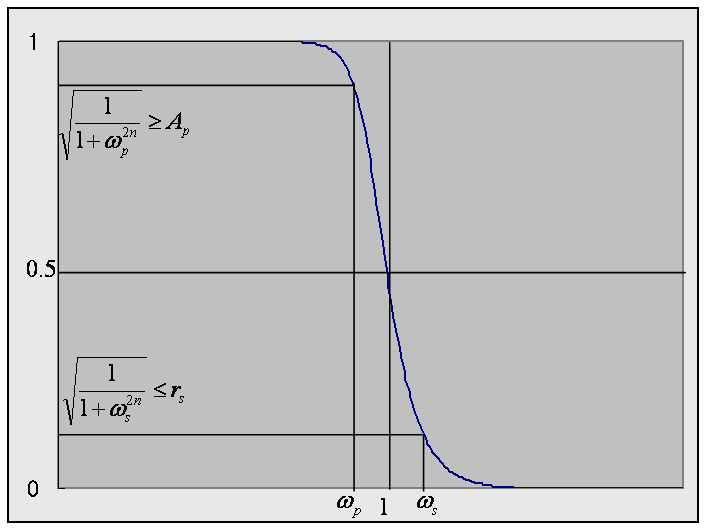 バターワースフィルタの設計仕様
バターワースフィルタの設計仕様
このような次数 N を求めるためには、
図3に示すように、
という条件を満たすような最小の N を求めます。
これらの式から、
という式が得られるので、
これらの最大値を選ぶことにより、
という式が得られます。
この不等式を満たすような最小の N を選びます。
「アナログプロトタイプの設計」で得られた式を、
カットオフ周波数ωcで双1次変換することで以下の式が得られます。
c = cos ωc ,
s = sin ωc
H
(z
)
=
| ()(
1 + 2 z-1 + z-2) |
| (1+αk, n)
-
2 c z-1
+
(1-αk, n)
z-2 |
,
(nが偶数のとき)
H
(z
)
=
| s (1 + z-1) |
| (s + c + 1) + (s - c - 1) z-1 |
×
| ()(
1 + 2 z-1 + z-2) |
| (1+αk, n)
-
2 c z-1
+
(1-αk, n)
z-2 |
(nが奇数のとき)ただし、αk, n は以下の式で表される値です。
「周波数変換」で説明したように、
ローパスフィルタのアナログ伝達関数の変数 s を s → に入れ替えると、
ハイパスフィルタになります。
したがって、
ハイパスバターワースフィルタのアナログプロトタイプ伝達関数は以下のようになります。
この式の分母は、ローパス伝達関数の分母と全く同じものになっています。
(バターワースフィルタの伝達関数は、分母の定数項と2次の係数が同じなのでこうなる。)
その結果、ディジタルフィルタ伝達関数も、以下のように、
ローパス伝達関数と分母が全く同じものになります。
H
(z
)
=
| ()(
1 - 2 z-1 + z-2) |
| (1+αk, n)
-
2 c z-1
+
(1-αk, n)
z-2 |
(nが偶数のとき)
H
(z
)
=
| (1+c)(1 - z-1) |
| (s + c + 1) + (s - c - 1) z-1 |
×
| ()(
1 - 2 z-1 + z-2) |
| (1+αk, n)
-
2 c z-1
+
(1-αk, n)
z-2 |
(nが奇数のとき)この式を、ローパス伝達関数と見比べてみると、
分母が同じなだけでなく、
分子も似たものになっています。
式中で強調表示している部分の符号が異なっているだけです。
このことから、同じカットオフ周波数のローパス・ハイパスフィルタは、
その処理の大部分を共通化することができます。



