「チェビシェフフィルタ」や「逆チェビシェフフィルタ」は、
通過域または阻止域のどちらか一方で等リプルとなるようすることで、
「バターワースフィルタ」よりも急峻なカットオフ特性を得ていました。
それに対して、
通過域と阻止域の両方で等リプルとなるようにすることで、
より急峻なカットオフ特性を得ようという考え方の基に作られたのが
楕円フィルタ(elliptic filter)です。
このような特性を持ったフィルタを設計するためには、
楕円関数の知識を要するので、楕円フィルタという名前で呼ばれています。
また、楕円フィルタは、
チェビシェフ特性と逆チェビシェフ特性の考え方を連立して考えるという意味で、
連立チェビシェフフィルタと呼ばれることや、
考案者の名前を取って、Cauerフィルタと呼ばれることもあります。
 透過域と阻止域の両方にリプル
透過域と阻止域の両方にリプル
チェビシェフ多項式 Cn(ω) や、
その逆 1 / Cn(1/ω) の代わりに、
表1に示すような特徴を持つn次有理式 Rn, k1(ω) を考えます。
チェビシェフ多項式の拡張
|
|
Cn(ω)
|
1 / Cn(1/ω)
|
Rn, k1(ω)
|
|
ω ≦ 1のとき
|
n個の零点を持っていて、-1 ~ 1の間で振動
|
緩やかに単調増加
|
n個の零点を持っていて、-1 ~ 1の間で振動
|
|
ω > 1のとき
|
急激に単調増加
|
n個の極を持っていて、 絶対値が1 ~ ∞の間で振動
|
n個の極を持っていて、 絶対値が1/k1 ~ ∞の間で振動 (k1は定数)
|
このような有理式 Rn, k1(ω) を使って、
以下のような周波数特性を作ってやれば、
通過域と阻止域の両方で等リプルとなるよな特性が得られます。
このようにして得られる周波数特性を楕円特性と呼び、
楕円特性 HE(ω) は、
チェビシェフ特性 HC(ω) や逆チェビシェフ特性 HI(ω) と比べると、表2に示すような特性になります。
楕円特性の要点
|
|
チェビシェフ特性HC(ω)
|
逆チェビシェフ特性HI(ω)
|
楕円特性HE(ω)
|
|
ω ≦ 1のとき
|
1 ~ の間で振動
|
緩やかに単調減少(1に近い値)
|
1 ~ の間で振動
|
|
ω > 1のとき
|
急激に単調減少
|
0 ~ の間で振動
|
0 ~ の間で振動
|
楕円フィルタの発想は極めて単純ですが、
上述のような特長を持つ有理式 Rn, k1(ω) をどのようにして作るかが問題となります。
このような有理式の作り方を次節で説明します。
以下のようにして有理式 Rn, k1(x) を定義することで、
「基本アイディア」で述べたような特徴を持つ有利式が得られ、
この有理式を「チェビシェフ有理関数」 と呼びます。
R
n, k1(x
)
=
cd(cd-1(
x,
k
)
,
k
1)チェビシェフ有理関数は一見すると複雑に見えますが、
n個の零点とn個の極を持ち、
以下のようなn次の有理式で表すことが出来ます。
Rn, k1(x)
=
x
| x2 - ωm, n2 |
| k2 ωm, n2 x2 - 1 |
… n が奇数のとき
Rn, k1(x)
=
| x2 - ωm, n2 |
| k2 ωm, n2 x2 - 1 |
… n が偶数のとき
ただし、
ωm, n =
sn(K,
k
)
です。
チェビシェフ有理関数の詳細について説明すると長くなりますので、
別項 「チェビシェフ有理関数」 で説明します。
上式中の k, k1 などのパラメータの意味についても
「チェビシェフ有理関数」 を参照してください。
以下の図に、例として、3次、5次、9次の楕円フィルタの振幅特性を示します。
この例では、リプル幅は 0.1 で設計しています。
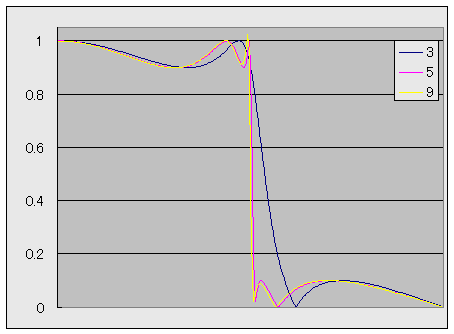 3~9次の楕円フィルタの周波数特性
3~9次の楕円フィルタの周波数特性
Rn, k1(ω) の極が
HE(ω) の零点になります。
cd(u, k) の極は
(2 m + 1) K + i K1' なので、
Rn, k1(ω) の極は、
cd
-1
(ω, k
)
=
(2 m + 1
) K
1 + i K
1'
(m は任意の自然数。)
の解になります。
これを解くことにより、
が得られます。
ラプラス変数 s = i ω で表すと、
伝達関数の零点 s は以下のようになります。
ただし、kは0~(n-1) / 2までの整数です。
HE(ω) の極は、
R
n, k1(ω
)
=
cd(cd-1(
ω,
k
)
,
k
1)
=
±i
を解くことで得られます。
cd-1(ω, k)
=
u + i v
と置くと、
cd
(
(u + i v
)
,
k
1)
=
±i
となります。
ここで、
sn =
sn( u - K1 , k1),
sn' =
sn( v , k1'
)
などと置くと、ヤコビの楕円関数の加法定理より、
|
sn dn' + i cn dn sn' cn'
|
|
cn'2 + k12 sn2 sn'2 |
=
±i
となります。
右辺の実部が0、かつ、
dn' は常に非0なので、
sn =
sn( u - K
1 , k
1)
=
0
が得られ、したがって、
u - K
1
=
2 m K
1
(m は任意の自然数。)
が得られます。
このとき、cn = dn = 0 なので、
よって、
これらの結果をら、
cd-1(ω, k)
=
u + i v
に代入することで、解 ω が得られます。
sn =
sn(u, k),
sn' =
sn(v, k'),
などと置くと、
ω
=
|
sn dn' ± i cn dn sn' cn'
|
|
1 - dn2 sn'2 |
となります。
この中から安定極のみを選ぶことで、伝達関数の極 s は以下のようになります
s
=
|
- cn dn sn' cn'
± i sn dn'
|
|
1 - dn2 sn'2 |
sn
=
sn(
K
,
k
)
(cn, dn
も同様)
sn'
=
sn(sc-1()
,
k'
)
(cn', dn'
も同様)
ただし、
kは
0~(n-1) / 2までの整数です。
透過域/阻止域の周波数/リプル
(Ap, rs, ωs)
を仕様として与えたとき、
仕様を満たす最小の次数 N とパラメータ ε, k1 を求める方法について説明します。
(ωp は 1 で固定。)
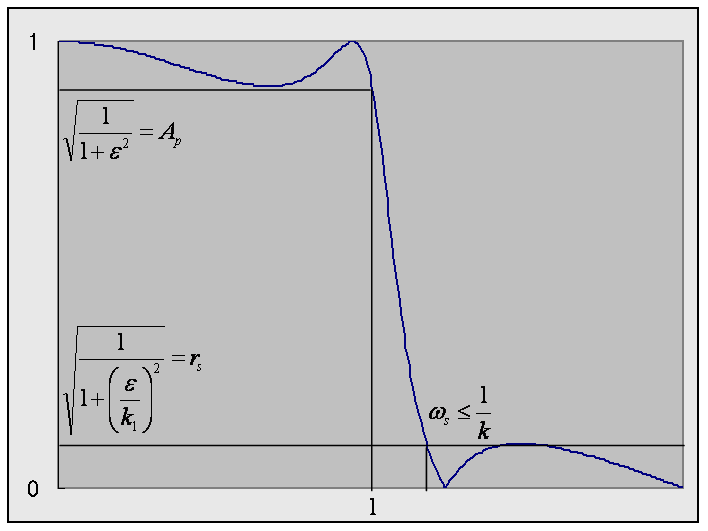 楕円フィルタの設計仕様
楕円フィルタの設計仕様
まず、透過域リプルから ε を決定します。
図4に示すように、
=
Ap2
なので、
が得られます。
次に、阻止域リプルから k1 を決定します。
=
rs2
なので、
が得られます。
また、
ωs ≦
および
楕円積分の性質
(K(x) は単調増加、
K' (x) は単調減少)を用いると、
となり、
この式を満たすような最小の N を選びます。
そして最後に、
N
=
となるような k を求めます。



