発散とはある点における単位体積あたりのベクトル場の湧き出し(「流束」参照)の量、つまり湧き出しの密度
です。
発散という言葉は、ある点から湧き出したベクトル場が外に向かって広がっていくという意味で使われています。
すなわち、ある点Pにおけるベクトル場
F
の発散
div
F
とは、点Pを囲む任意の閉曲面をS、その内部の体積をVとすると、
で定義されます。
また、
div
F
は
∇・
F
とも書きます
。
これだけでは分かりにくいでしょうからもう少し直感的な発散の意味を言うと、
発散とは
面積分(「面積分とは」参照)と体積積分(「体積積分とは」参照)を関係付ける微分演算
で、直交座標を用いて表すと
となります。
ただし、
F = (
Fx, Fy, Fz
)
です。
∇・
F
という書き方をするのは、ナブラベクトル
∇ = (
,,
)
と
F
の内積を取ったものが発散となるからです。
発散は湧き出しの密度なわけですから発散を体積積分したものは湧き出しに等しくなります。
つまり、
この式をガウスの定理といい、面積分と体積積分を関係付ける公式です。
図1のような微小体積を考えると、その表面を貫いて外に出て行くベクトル場
F
の流束は
{
Fx(x,y,z)−Fx(x+dx,y,z)
}
dydz+{
Fy(x,y,z)−Fy(x,y+dy,z)
}dzdx+{
Fz(x,y,z)−Fz(x,y,z+dz)
}dxdy
となります。
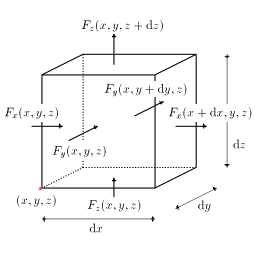 微小体積
微小体積
ここで、
Fx(x,y,z)−Fx(x+dx,y,z) = dx
であることを用いると、この式の第一項は
dV
となります(
dV=dxdydz
)。
同様に第二項、第三項も
dV, dV
となりますので、左図の微小体積の表面を貫く
F
の流束は
となります。
そして発散の定義から、
となります。

