磁場と磁束密度
電場と電束密度と同じように、磁気に関する場にも、磁場と磁束密度の2つのものがあります。 磁荷(磁気単極子)というものが存在するなら電場と同じように磁場を説明出来るのですが、 残念ならが磁荷というものは存在しません。 電場が電荷から生じるように、 磁場というものは電場の変化や、電荷の運動によって生じます。 それでは磁場と磁束密度について解説していきます。
磁場というのは自由電流の周りに生じる渦状の場(「渦」)です 。 渦の強さは電流の大きさに比例し、渦の回転軸は電流の向きを向いています。 すなわち、自由電流密度 J の周りに、
を満たすように生じる場 H が磁場です。
一方で、磁束密度は2本の電流の間に働く力を近接作用で考える(つまり、電流が存在するところには何らかの場が発生して、その場が他の電流に力を加えると考える)際に利用する場です。 すなわち、電流の周りには磁束密度が発生し、磁束密度 B の中に速度 v で動く電荷qをおくと、
という力が発生するするというものです。
そして、この2つの量の間には比例関係が成り立ちますから、比例係数 μ0 を定義して
という関係が成り立ちます。 ここで用いた比例係数 μ0 を 真空中の透磁率 といいます。
磁性体
磁性体とは、磁場をかけると磁化を起こして磁化電流の現れる物質のことです。
磁化とは、磁性体中にある電子の角運動量やスピンによって生じる電流の微小ループ(これを磁気双極子という。左図参照。)の向きがそろって分布している状態のことを言います。 磁性体に磁場をかけることで、磁性対中の電子のスピンや角運動量の向きがそろい、このような状態が生じます。 このような、磁気双極子の分布によって磁性体中に電流の分布が生じます。 この磁化によって生じる電流密度分布を磁化電流密度といいます。
磁気双極子に対して、磁気双極子モーメント m というものを定義し、
で表します。 ここで、Iは電流の強さで、Sは電流の流れるループの内部の面積、 n はこの面の法線ベクトルです。 なぜこの式で磁気双極子を表すかというと、このような磁気双極子に対して磁束密度 B をかけると、磁気双極子を磁束密度と同じ向きに向けようとするトルク(偶力) T がはたらき、 T = m×B と表せるからです。
次に、磁化は磁気双極子の密度ですから、磁気双極子の分布密度をNとすると、 磁化密度 M は
となります。
そして、磁化によって生じる磁化電流 J m は
となります。
磁性体中の磁場・磁束密度
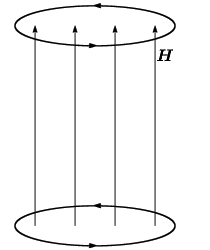
磁場 H は自由電流密度(つまり、磁性体に生じた磁化電流密度は考慮に入れない)から発生する渦です。 要するに、磁場は磁性体中でもその値は変わりません。 また、磁性体に磁場をかけると磁化 M が生じます。 この様子を下図1、2に示します。
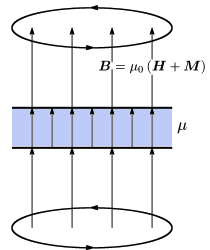
一方、磁束密度 B は、動いている電荷にかかる正味の力をあらわすものですから、 磁性体に生じた磁化の分まで考慮に入れる必要があります。 すなわち、磁性体中では磁場は変化し、
という関係が成り立ちます。 この様子を下図3に示します。
|

|
|
さて、ここで磁化密度が磁性体にかけた磁場に等方線形時不変で比例すると仮定します(この仮定はどんな磁性体に対しても出来るわけではありませんが、たいていは出来るものとみなして大丈夫です。ただ、磁性体には磁場をかけなくても磁化したままになる強磁性体というものも存在します)。 この仮定の元、 H = χmM と置くと、
となります。 ここで用いた比例係数 χm を磁化率といい、 μ を(磁性体中の)透磁率といいます。 また、 μr = 1+χm というものを定義し( μ = μrμ0 )、これを比透磁率といいます。
E⇔H対応とE⇔B対応
もし、単磁荷(磁気双極子)というものが存在するのなら、
E
⇔
H
、
D
⇔
B
という対応が最も自然なものとなるでしょう。
そこで、このような単磁荷が存在するものと仮定し、
2つの電荷
q1, q2
に電場に関するクーロンの法則
F =
が成り立つことに対し、
2つの磁荷
m1, m2
に磁場に関するクーロンの法則
F =
q1q2
4
が成り立つとして電磁理論を構成する考え方もあります(高校の教科書に出てくる電磁理論はまさにこれ)。
このように、
E
と
H
を対比させて考える方法をE⇔H対応と言います。
m1m2
4
単磁荷というものは存在しませんが、 電気双極子(電場をかけると T = p×E というトルクが発生する)と 磁気双極子(磁場をかけると T = m×μH というトルクが発生する)が式の上で非常に似ていることと、 誘電体中では分極によって ρp = −∇・P という分極電荷密度が発生することから、 磁性体中には仮想的に ρm = −∇・μ0M という磁荷密度が発生すると考えることができます。
しかし、実際には磁気は電流によって生じるものですし、 電気では「電荷によって電束密度が生じ、電場中に電荷を置くと力を受ける」と考えますが、 磁気では「電流によって磁場が生じ、磁束密度中で電荷を動かすと力を受ける」と考えたほうが、わざわざ磁荷という存在しない仮想的な量を考えなくて済む分、 分かりやすいので、普通はこのように E と B を基本として理論を立てます。 このような考え方をE⇔B対応と言います。

