概要
ベクトルというのは元々は物理学で空間上の位置、速度、加速度などを表すためにできたものです。 これは現在では幾何ベクトル(geometric vector)と呼ばれているものに相当します。
これに対して、現在では、幾何ベクトルのある性質(線形性)と同じ性質を持つような集合を抽象的にとらえて考えます。 そのような集合を線形空間(linear space)あるいはベクトル空間(vector space)と呼び、 線形空間上における数学的議論を線形代数(linear algebra)と呼びます。
ベクトル
ここではまず、元々の意味でのベクトル、 すなわち、向きと大きさを持つ量としてのベクトルについて復習しましょう。
幾何ベクトル
高校数学などで最初に習う、 向きと大きさを持つ量を幾何学的なイメージで捉えたものを幾何ベクトル(geometric vector)と呼びます。
すなわち、幾何ベクトルは、図1のように、原点から伸びる矢印で表されます。 図2のように、平行移動すると一致するような2つのベクトルは等しいと考えます。
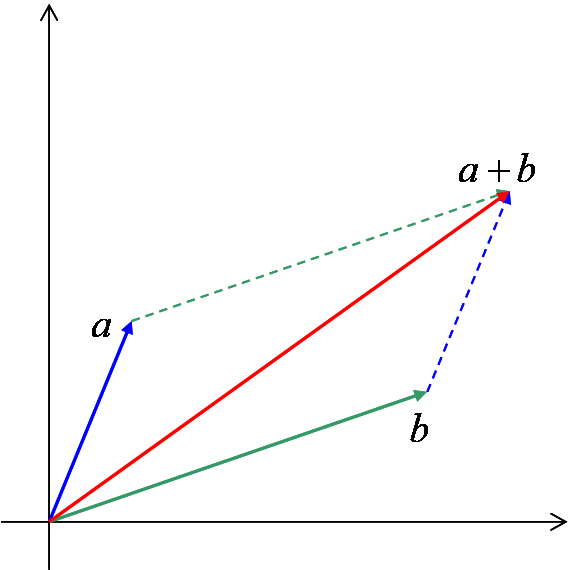
このような矢印に対して、以下のようにして、 和と定数倍を定義します。
-
和a + b: 2つの矢印a, bを繋ぎ合わせる(図3)
-
定数倍k a: 矢印aを倍率kで拡大/縮小(図4)
ここで、向きと大きさを持った量であるベクトルに対して、 大きさのみを持つ量をスカラー(scalar)と呼び、 上述の定数倍はスカラー倍と呼ぶことも多いです。
数ベクトル
K を実数または複素数全体の集合として、 K の元の組(「順序対」)に対して、 以下のようにして和と定数倍(スラカー倍)を定義したものを数ベクトル(numeric vector)と呼びます。
-
和 a + b = ( a1 + b1 , a2 + b2 , a3 + b3)
-
定数倍 k a = ( k a1 , k a2 , k a3)
平行線の公理(直線と、その上にない1点に対し、その点を通り直線と平行な直線がただ1つ存在する)の元で、「幾何ベクトル」に対して適当な座標を導入することで、 幾何ベクトルと1対1に対応する数ベクトルができます。 数ベクトルの和・定数倍は、 それぞれに対応する幾何ベクトルの和・定数倍に一致します。
線形空間
幾何ベクトルや、数ベクトルという具体的なものから離れて、 ベクトルの持つ、線形性という特徴に着目して、 抽象化した概念を 線形空間(linear space) あるいはベクトル空間(vector space)と呼びます。
すなわち、 「体」K に対して、 a, b ∈ K, x, y ∈ V のとき、 和 x + y と スカラー倍 a x が定義できて、
という性質を満たすような集合 V が線形空間です。 このような性質を線形性(linearity)と呼びます。
例
抽象的に捕らえることで、さまざまなものが線形空間とみなせるようになります。
微分方程式の解
x1 , x2 がいずれも微分方程式
| d 2 |
| dt2 |
| d |
| dt |
の解のとき、 その線形結合 a x1 + b x2(ただし、a, b ∈ C)もこの微分方程式の解となります。 したがって、この手の微分方程式の解は線形空間をなします。
一般に、x とその(高階)微分の1次式になっている微分方程式の解は線形空間になります。
多項式
f1 , f2 が実係数 n 次多項式のとき、 a f1 + b f2(ただし、a, b ∈ R)も実係数 n 次多項式になります。 したがって、 n 次多項式全体の集合は線形空間をなします。
次元
体 K 上の線形空間 V の m 個の元 vi ∈ V (i = 1 ~ m)に対し、
| m |
| ∑ |
| i = 1 |
となるような K の元 ai が存在するとき、 vi は線形従属(linear dependent)であるといい、 そうでないとき線形独立(linear indipendent)であるといいます。
線形空間 V において、 N 個のベクトルまでは線形独立 ( ∀ ai ∈ K s.t.
| N |
| ∑ |
| i = 1 |
ai vi ≠ 0 ) にできて、 N + 1 個のベクトルになると必ず線形従属 ( ∃ ai ∈ K s.t.
| N + 1 |
| ∑ |
| i = 1 |
ai vi = 0 ) になるような自然数 N が存在するとき、 N を V の次元(dimension)と呼びます。
基底
「数ベクトル」で、 「幾何ベクトル」に適当な座標系を与えたものが「数ベクトル」だと説明しましたが、 座標系(coordinate system)の与え方は1通りではありません。
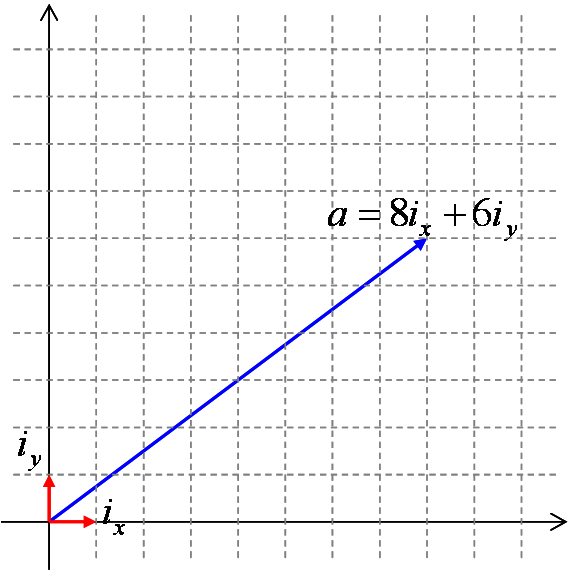
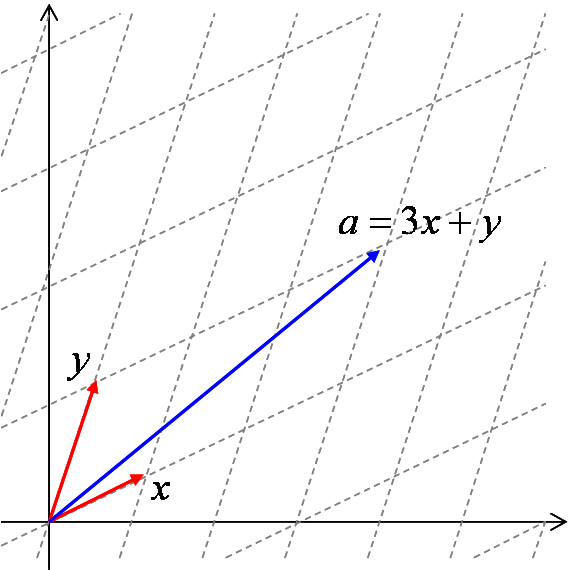
座標系として最もよく用いられるのは、 図5に示すような、直交座標系ですが、 別にこのような座標系の取り方以外にも、いくらでも座標系の取り方があります。 例えば、図6のように、適当に選んだ2つのベクトル x, y を使って幾何ベクトルを表すことも出来ます。
さて、このとき、 図5の場合なら ix , iy、 図6の場合なら x, y を座標系の基底(base)といいます。 あるいは、逆に、 {ix , iy} や {x, y} 等の、 基底の組自体を座標系と呼びます。
図5の場合、a を座標系 {ix , iy} で表すと、その座標が (8, 6)。 図6の場合、a を座標系 {x, y} で表すと、その座標が (3, 1)、ということになります。
ちなみに、任意の(有限次元の)線形空間は、適当な座標系を導入することで、数ベクトルとして表すことができます。
余談
余談1
力学等の、ベクトルが用いられる多くの分野では、 ベクトルの絶対値や内積が頻出します。 しかしながら、線形空間の定義には絶対値や内積の定義は含まれません。 これらの定義できるような集合は、 距離空間や内積空間と呼ばれます。
これは要するに、 まずは線形性という特徴にだけ着目し、線形性を持つ集合の性質を十分に考察してから、 別途、絶対値や内積を定義できる集合を考察しようということです。
余談2
「体」 K 上の線形空間と同様にして、 体 K の代わりに「環」R を使って定義したものを R-加群といいます。 体よりも環のほうが条件がゆるいので、 線形空間よりも加群のほうが条件のゆるい集合になります。
線形空間に対する定理の中には、 加群に対しても成立するものもあれば、 そうでないものもあり、 加群に関する考察も1つの数学の分野となっています。
余談3
複素数は実数上の2次元線形空間とみなすこともできます。 詳しくは「体の拡大」で説明しますが、 一般に、 体 K の代数拡大体 F は、 K 上の線形空間になります。