2分探索木

キーワード

2分探索木

概要

一般に木構造というと、循環のない有向グラフのことなんですが、そういう一般論はまた別の機会に話をしましょう。

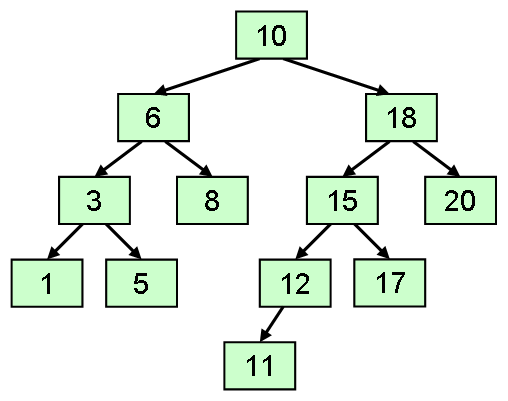
ここでは、要素の挿入・削除・検索を高速に行うことの出来るコレクションのデータ構造として、 2分探索木（binary search tree）というものを紹介します。 2分探索木は、以下のような特徴を持つ木構造です（図1）。

2分木（各ノードは最大で2本の子を持つ）。
全ての要素が「左の子＜親≦右の子」（あるいは「左の子≦親＜右の子」）という大小関係を満たす。

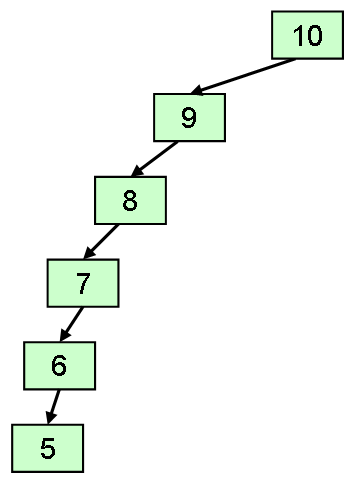
要素の挿入・削除・検索は、木の根から葉までの経路を1つ探索することになるので、木の高さ分に比例する計算量が必要です。理想的には、木のバランスが均等に整っていれば、要素数を n として計算量は O(log n) になります。しかしながら、逆に、図2に示すように、木が左右どちらかに偏っている場合、計算量は O(n) になります。

特徴

2分探索木は以下のような利点を持っています。

理想的には、要素の挿入・削除・検索が O(log n) で行える。
「ハッシュテーブル」のように、メモリを多めに確保しておく必要がない。
また、ハッシュ関数の作り方に悩む必要もない。
要素を整列された順序で取り出せる。

ただし、以下のような欠点もあります。

木の高さがバランスを保っていないと検索などが O(n) になる。平衡化機構が必要。

ちなみに、2分探索木への、平衡化機構の組込み方にはいくつか種類があります。実装が簡単なのでよく用いられる物としては、赤黒木あるいは2色木（red-black tree）と呼ばれるものがあります。

2分探索木の実装

まず、2分探索木も構造的には2分木なので、以下のような左右の子を持つノードを定義します。

public class Node
{
  #region フィールド

  internal T val;
  internal Node left, right, parent;

  internal Node() : this(default(T), null) { }

  internal Node(T val, Node parent)
  {
    this.val = val;
    this.parent = parent;
    this.left = this.right = null;
  }
}

「連結リスト」と同様に、 left、 right 等の「アクセスレベル」は internal にしておきます。

そして、2分探索木には、木の根に当たるノードを持つための変数を用意します。

class BinaryTree<T> : IEnumerable<T>
  where T: IComparable<T>
{
  Node root;
}

前節で説明したような条件を満たす2分探索木中の要素を検索するには、以下のようにします。要するに、値の大小を見て、左の子を見るか右の子を見るか決めて、木を根から葉に向かってたどります。

public Node Find(T elem)
{
  Node n = this.root;
  while (n != null)
  {
    if (n.val.CompareTo(elem) > 0) n = n.left;
    else if (n.val.CompareTo(elem) < 0) n = n.right;
    else break;
  }
  return n;
}

次に、要素の挿入ですが、とりあえず、平衡化することは考えなければ、実装方法は簡単で、検索のときと同じ要領で木の中を探索し、新しい葉を作ります。

public void Insert(T elem)
{
  if (this.root == null)
  {
    this.root = new Node(elem, null);
    return;
  }

  Node n = this.root;
  Node p = null;
  while (n != null)
  {
    p = n;
    if (n.val.CompareTo(elem) > 0) n = n.left;
    else n = n.right;
  }

  n = new Node(elem, p);
  if (p.val.CompareTo(elem) > 0) p.left = n;
  else p.right = n;
}

ノードの削除も、平衡化のことを考えなければ、以下のようにして簡単に行えます。

左の子が null なら、自身の位置に右の子ノードを繋ぎなおす。
右の子が null なら、自身の位置に左の子ノードを繋ぎなおす。
両方の子が非 null なら、自身の次に大きな値を持つノード（右の部分木の左端）で自身を置き換える。

public void Erase(Node n)
{
  if (n == null) return;

  if (n.left == null) this.Replace(n, n.right);
  else if(n.right == null) this.Replace(n, n.left);
  else
  {
    Node m = n.right.Min;
    n.Value = m.Value;
    this.Replace(m, m.right);
  }
}

/// <summary>
/// n の片方の子は null、もう片方の子は m という前提の元で、
/// ノード n の位置を子ノード m で置き換える。
/// </summary>
/// <param name="n">削除するノード</param>
/// <param name="m">置き換える子ノード</param>
void Replace(Node n, Node m)
{
  Node p = n.parent;
  if (m != null) m.parent = p;
  if (n == this.root) this.root = m;
  else if (p.left == n) p.left = m;
  else p.right = m;
}

public class Node
{
  /// <summary>
  /// このノード以下の部分木中で、最小の要素を持つノード（＝左端ノード）を返す。
  /// </summary>
  internal Node Min
  {
    get
    {
      Node n = this;
      for (; n.left != null; n = n.left) ;
      return n;
    }
  }
}