今日は、MathクラスのAtan2メソッドの話。あんまり数学がわかってない人だと、「tanの逆関数」なのにどうして2引数あるのかとか、AtanとAtan2で戻り値の範囲が違う(前者が-90度～90度、後者が-180度から180度)のが不思議だったりするみたいですね。

大元をたどるとatan2はFORTRANとかC言語とかの頃からあって、ちょっと調べれる範囲でもFORTRAN 77の時点であったらしいので、少なくとも1977年より前まで遡ります。なのでC#の小ネタというよりはプログラミング全般の小ネタだったり、むしろ、単に数学の話だったり。

x軸とのなす角

単純化のために、まずは半径1の円周上の点(x, y)の1点だけを考えて、原点からこの点までの線分と、x軸がなす角を考えます。以下の絵のような感じ。

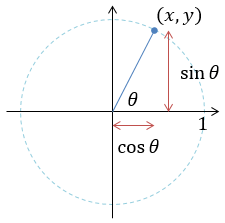
この絵を見ての通り、以下の条件を満たすθを計算することになります。

$x=\cos \theta$

$y=\sin \theta$

「逆三角関数を使えば簡単」と思うかもしれませんが、それだと半分だけ正解。$\theta ={\cos }^{-1}x$だと、x軸を中心に左右どちら周りなのかがわからなくなります。

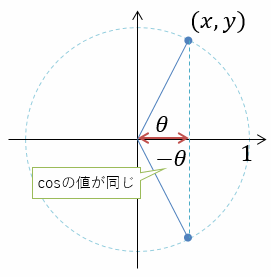
同様に、$\theta ={\sin }^{-1}y$だとy軸中心の折り返しがわからないです。さらにいうと、以下の式もダメ。y/xしている時点でわかると思いますが、符号が消えます。x, yともに正の場合と、共に負の場合が同じ値になってしまうので、やっぱり半円分しか計算できません。

$\frac{y}{x}=\tan \theta$

$\theta ={\tan }^{-1}\frac{y}{x}$

ということで、角度θを360度ちゃんと求めるためには、x, y、すなわち、cos, sinの両方の値が必要です。実際、Atan2は大体以下のような感じの分岐をしています。

static double Atan2(double y, double x)
{
    var z = Math.Atan(Math.Abs(y / x));
    if (x > 0)
    {
        if (y > 0) return z;
        else return -z;
    }
    else
    {
        if (y > 0) return Math.PI - z;
        else return z - Math.PI;
    }
    // ほんとは0, infinity, NaN の場合分けあり
}

2点のなす角

ここからは完全におまけ。ちょっとした数学の話。2点だとどうでしょう。(x₁, y₁)と原点と(x₂, y₂)のなす角。

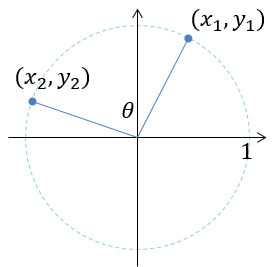
これも、正弦定理・余弦定理からの変形で、以下のような式が成り立ちます。

$\cos \theta =x_1{x}_2+y_1{y}_2$

$\sin \theta =x_1{y}_2-x_2{y}_1$

内積がcosで、面積(交代積)がsin。これらをAtan2(sin, cos)の順で与えれば角度θが求まります。

オイラーの公式

もう1つおまけ。 「オイラーは数多の公式を残しすぎてどの公式だよ」という話もあるんですが、ここで話すのは複素解析におけるオイラーの公式です。有名なあれ。 $e^{i\theta }=\cos \theta +i\sin \theta$

これを逆に、$\cos \theta +i\sin \theta =x+iy$だと考えた場合、両辺の対数を取ることで、

$i\theta =\log \left(x+iy\right)$

$\theta =-i\log \left(x+iy\right)$

となります。 ここで、Atan2の使い道を思い出してみます。θ=Atan2(y, x)なわけで、

$\mathrm{Atan}2\left(y, x\right)=-i\log \left(x+iy\right)$

です。Atan2は、絶対値が1の複素数に対する対数関数と関連していたりします(指数関数が三角関数と関連しているんだから、対数関数(指数関数の逆関数)が逆三角関数と関連しているのも当然の話です)。

てことで、実のところ、Atan2って、「複素対数関数」だと言っても過言ではなかったり。 実装都合の変な関数ではなくて、割かし「数学的にあり得る関数」です。